La definizione di matrici simili è la seguente: due matrici. E. sono simili (o simili) se esiste una matrice. con cui è soddisfatta la seguente condizione: O equivalente: In effetti, la matrice. funge da matrice di cambiamento di base. Pertanto, ciò che significa questa equazione è che la matrice.. Per vedere se due matrici sono simili, possiamo utilizzare diversi metodi. Uno dei modi più comuni è il confronto delle forme canoniche di Jordan delle due matrici. Questo metodo coinvolge la decomposizione delle matrici in blocchi di Jordan e il confronto dei blocchi corrispondenti per vedere se sono uguali.. Quando due matrici hanno lo.

Come determinare se due rette sono parallele YouTube

PPT Le figure piane PowerPoint Presentation, free download ID5558601

3 Modi per Determinare se Due Rette sono Parallele

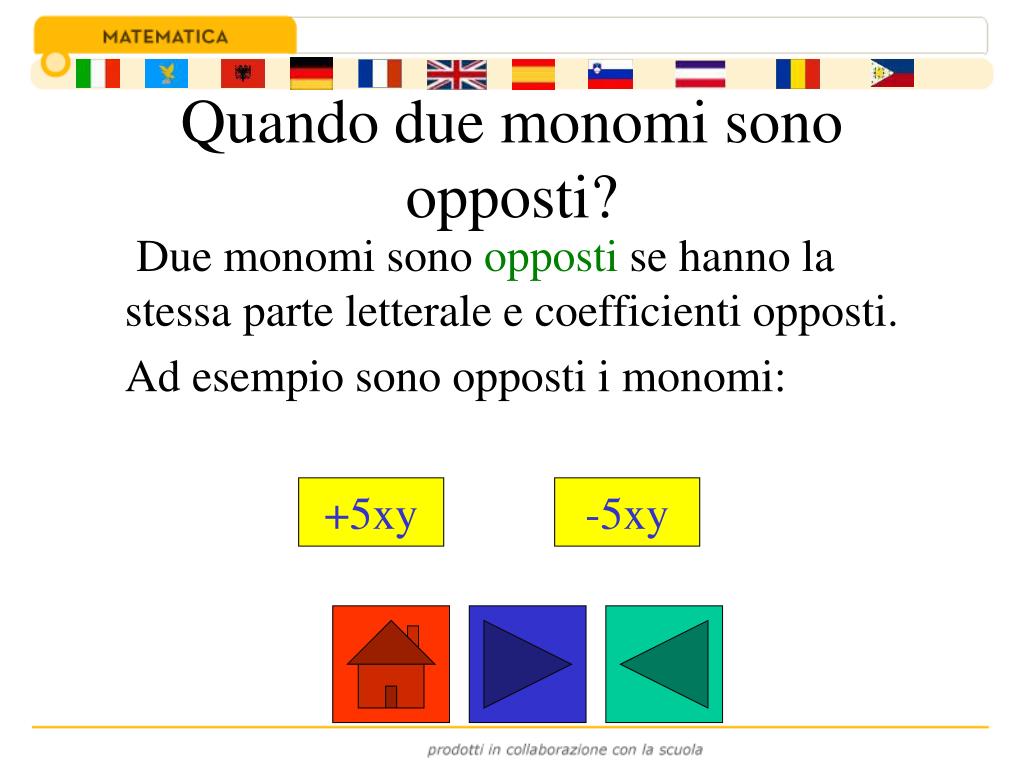
PPT I monomi PowerPoint Presentation, free download ID5508551

Matrici Simili E Diagonali 1 Matrici simili e matrici diagonalizzabili Matrici simili Sia V

Matrici diagonalizzabili ( con esercizio d'esame svolto ) YouTube

OPERAZIONI CON LE MATRICI Andrea il Matematico

Somma di due matrici

Quando due rette sono parallele Lettera43 Come Fare

Teoria delle matrici definizioni YouTube

Domande gal seconda parte Quando due matrici si dicono simili? Che importanza ha il concetto

36.Matrici Simili, Diagonalizzazione, Radici Polinomio, Molteplicità Autovalore

Matrici e trasformazioni Rai Cultura

Come svolgere operazioni con le matrici YouTube

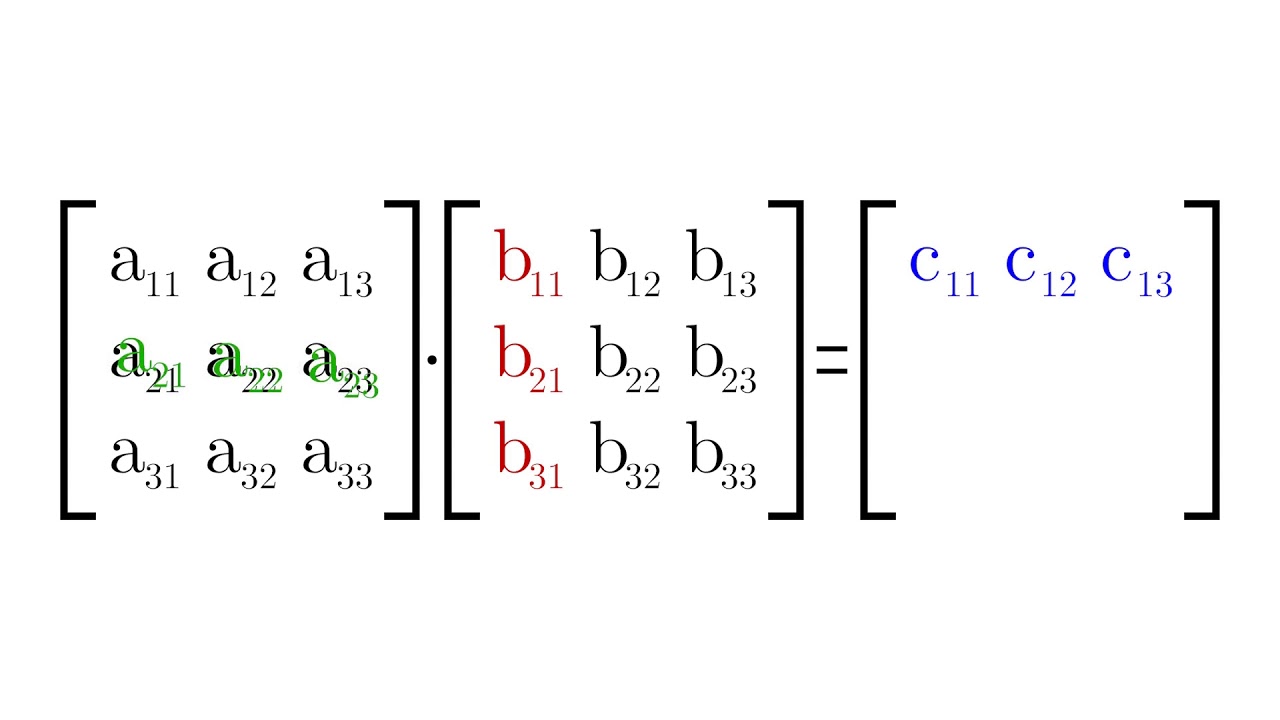
Composizione (prodotto) di due matrici YouTube

Quando DUE RETTE sono PERPENDICOLARI? MondoFisica

Cosa succede quando due marchi sono simili YouTube

Econometria le matrici Dispense

MATRICI SOMMA E DIFFERENZA TRA DUE O PIU' MATRICI YouTube

PPT Matrici PowerPoint Presentation, free download ID5027289

Definizione. Due matrici quadrate e sono simili quando esiste una matrice invertibile tale che: = In particolare, la matrice identità e la matrice nulla sono simili solo a loro stesse.. Invarianti per similitudine. Due matrici simili hanno lo stesso rango, determinante e traccia.Si dice quindi che rango, determinante e traccia sono invarianti per similitudine.. Suggerimento: vi sono due modi per dare la dimostrazione: primo modo: pensare che due matrici sono simili se e solo se sono associate ad uno stesso endomorfismo relativamente a basi differenti secondo modo: usare una dimostrazione analoga a quella data per dimostrare che due matrici simili hanno lo stesso polinomio caratteristico.