[Solved] Prove the general arithmeticgeometric mean 9to5Science

Of great significance is the arithmetic-geometric mean inequality. In operator theory, a lot of operator inequalities appear, some of which are related to the operator monotone or operator convex functions and Kubo-Ando theory [ 11 ], where the operator geometric mean \ (A \sharp B\), defined by \ (A^ {1/2} (A^ {-1/2} B A^ {-1/2})^ {1/2} A.. This approach is very similar to applying the trivial inequality. For example, if we know that a a and b b are real numbers such that ( a-b) ^ 2 = 0 (a − b)2 = 0, then we can immediately conclude that a=b a = b. This is because the trivial inequality states that x^2 \geq 0 x2 ≥ 0, with equality only when x = 0 x = 0.

(PDF) On the ArithmeticGeometric mean inequality

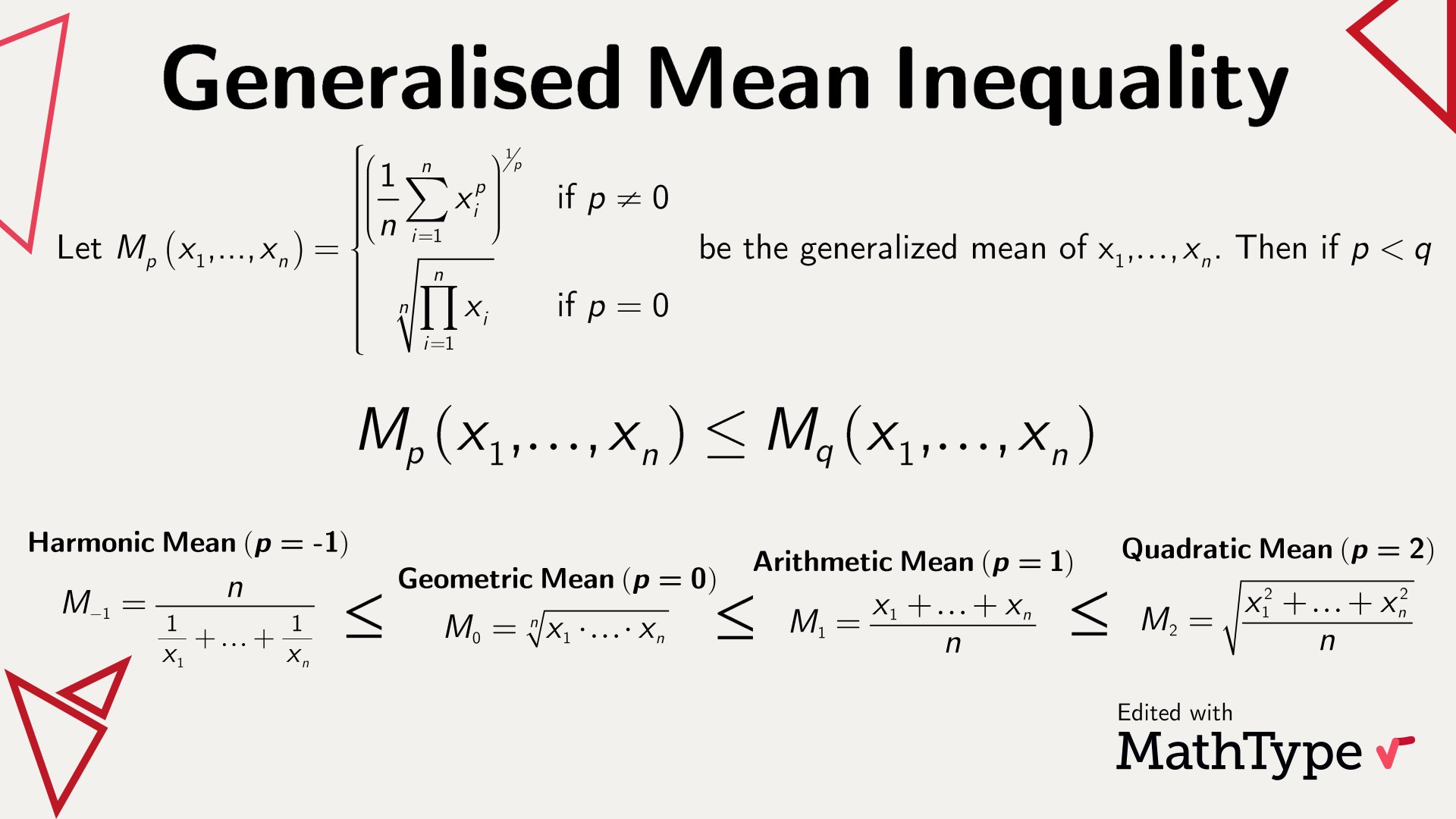
MathType on Twitter "The geometricarithmetic mean inequality and all other mean inequalities

Arithmetic Mean definition, formula and applicationsStatistical Aid

Inequalities 2 Relation Between Arithmetic Mean & Geometric Mean of Two Numbers YouTube

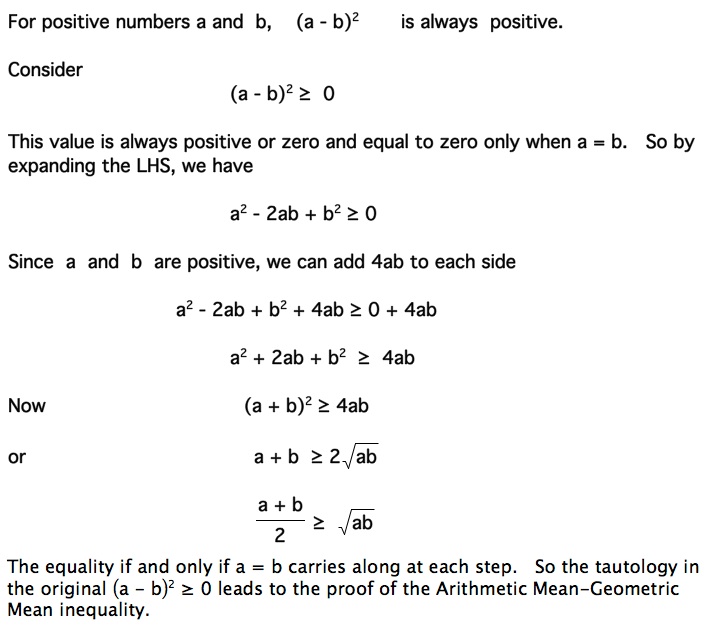
Using the Arithmetic MeanGeometric Mean Inequality in Problem Solving.

[Solved] Prove the general arithmeticgeometric mean 9to5Science

Prove the Inequality of Arithmetic and Geometric Means (AMGM inequality) Geometric mean

(PDF) Applications of Arithmetic Geometric Mean Inequality

Arithmetic Geometric Mean Inequality Proof by Induction and Calculus (1)

Solved 5. The arithmeticgeometric mean inequality. (a) Let

PPT Geometric Mean Theorem I PowerPoint Presentation, free download ID4868928

A SIMPLE PROOF OF THE GEOMETRICARITHMETIC MEAN INEQUALITY

Weighted arithmetic mean method

Arithmetic Mean Geometric Mean Inequality

PPT CauchySchwarz PowerPoint Presentation, free download ID3940924

11X1 T10 03 arithmetic & geometric means

Using the Arithmetic MeanGeometric Mean Inequality in Problem Solving.

(PDF) On a mixed arithmeticgeometric mean inequality

(PDF) Weighted arithmeticgeometric operator mean inequalities

Here are some special cases of the power mean inequality: • P 1 ≥ P 0 (the AM-GM inequality). • P 0 ≥ P −1 (the GM-HM inequality — HM is for "harmonic mean"). • P 1 ≥ P −1 (the AM-HM inequality). Date: November 7, 1999. 1The reason for this convention is that when r is very small but nonzero the value of P r is very close to. The QM-AM-GM-HM or QAGH inequality generalizes the basic result of the arithmetic mean-geometric mean (AM-GM) inequality, which compares the arithmetic mean (AM) and geometric mean (GM), to include a comparison of the quadratic mean (QM) and harmonic mean (HM), where.